Volver a Guía
Ir al curso
CURSO RELACIONADO
Física 03
2026
TORTI
¿Te está ayudando la guía resuelta?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰
Ir al curso
FÍSICA 03 UBA XXI
CÁTEDRA TORTI
Unidad 5
1.
Un libro de física que se desliza sobre una mesa horizontal a $1,10 \mathrm{~m} / \mathrm{s}$ cae y llega al piso en $0,350 \mathrm{~s}$. Ignore la resistencia del aire.
a) Calcule la altura de la mesa con respecto al piso.
a) Calcule la altura de la mesa con respecto al piso.
Respuesta
Si, este problema es un tiro oblícuo, no? Como ya te vengo avisando en toooodas estas guías, mi mejor recomendación es que vuelvas acá para seguir practicando con más ejercicios una vez que hayas visto todas las clases de tiro oblicuo del curso 😉
Reportar problema
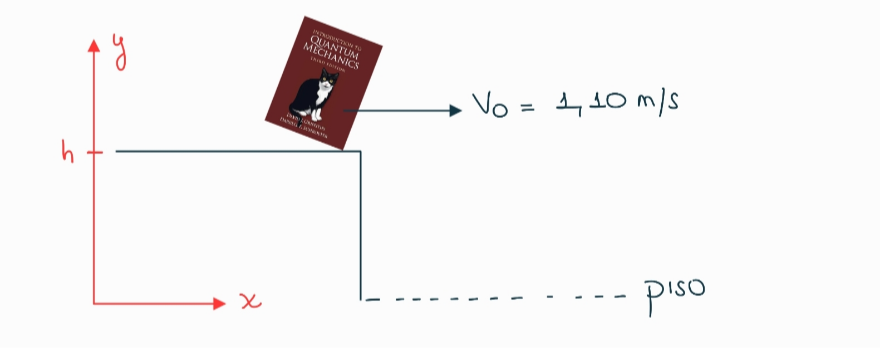
Ahora sí, vamos con este problema. Como siempre, me voy a hacer un esquema de la situación y elegir mi sistema de referencia:

En este caso, el libro tiene velocidad inicial únicamente en la dirección horizontal. Entonces,
$V_x = 1.10 \, \frac{m}{s}$
$V_{0y} = 0 \, \frac{m}{s}$
Las ecuaciones para el eje $x$ y el eje $y$ nos quedan así:
👉 Eje x: MRU
$x(t) = 1.10 \, \frac{m}{s} \cdot t$
👉 Eje y: MRUV
Para la posición en $y$ en función del tiempo:
$y(t) = y_0 + V_{0y} \cdot t + \frac{1}{2} \cdot a \cdot t^2$
En este caso, la altura inicial es una incógnita (que voy a llamar $h$, es la altura de la mesa), la velocidad inicial en $y$ es cero, y la aceleración gravitatoria es $g$ (que en nuestro sistema de referencia es negativa). Así que nos queda así:
$y(t) = h - 4.9 \, \frac{m}{s^2} \cdot t^2$
Perfecto, con esto arrancamos a responder las preguntas...
➡️ Altura de la mesa respecto al piso
Para calcular la altura de la mesa $(h)$, sabemos que el libro llega al piso (es decir, $y = 0$) en un tiempo $t = 0.350 \, \text{s}$. Usamos nuestra ecuación de posición en $y$ y planteamos que en $t = 0.350 \, \text{s}$, la posición $y$ es $0$
$h - 4.9 \, \frac{m}{s^2} \cdot (0.350 \, \text{s})^2 = 0$
Despejamos $h$
$h = 0.600 \, \text{m}$
Por lo tanto, la altura de la mesa con respecto al piso es de $0.600 \, \text{m}$.
🤖
¿Tenés dudas? Pregúntale a ExaBoti
Asistente de IA para resolver tus preguntas al instante🤖
¡Hola! Soy ExaBoti
Para chatear conmigo sobre este ejercicio necesitas iniciar sesión
ExaComunidad
Conecta con otros estudiantes y profesoresNo hay comentarios aún
¡Sé el primero en comentar!
